Pépin's test
In mathematics, Pépin's test is a primality test, which can be used to determine whether a Fermat number is prime. It is a variant of Proth's test. The test is named for a French mathematician, Théophile Pépin.
Contents |
Description of the test
Let 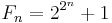 be the nth Fermat number. Pépin's test states that for n > 0,
be the nth Fermat number. Pépin's test states that for n > 0,
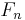 is prime if and only if
is prime if and only if 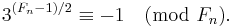
The expression 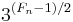 can be evaluated modulo
can be evaluated modulo 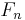 by repeated squaring. This makes the test a fast polynomial-time algorithm. However, Fermat numbers grow so rapidly that only a handful of Fermat numbers can be tested in a reasonable amount of time and space.
by repeated squaring. This makes the test a fast polynomial-time algorithm. However, Fermat numbers grow so rapidly that only a handful of Fermat numbers can be tested in a reasonable amount of time and space.
Other bases may be used in place of 3, for example 5, 6, 7, or 10 (sequence A129802 in OEIS).
Proof of correctness
For one direction, assume that the congruence
holds. Then  , thus the multiplicative order of 3 modulo
, thus the multiplicative order of 3 modulo 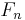 divides
divides 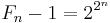 , which is a power of two. On the other hand, the order does not divide
, which is a power of two. On the other hand, the order does not divide 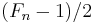 , and therefore it must be equal to
, and therefore it must be equal to 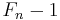 . In particular, there are at least
. In particular, there are at least 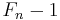 numbers below
numbers below 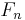 coprime to
coprime to 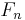 , and this can happen only if
, and this can happen only if 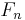 is prime.
is prime.
For the other direction, assume that 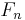 is prime. By Euler's criterion,
is prime. By Euler's criterion,
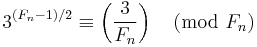 ,
,
where 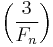 is the Legendre symbol. By repeated squaring, we find that
is the Legendre symbol. By repeated squaring, we find that 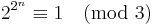 , thus
, thus 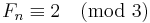 , and
, and 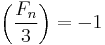 . As
. As 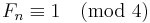 , we conclude
, we conclude 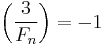 from the law of quadratic reciprocity.
from the law of quadratic reciprocity.
References
- P. Pépin, Sur la formule
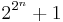 , Comptes Rendus Acad. Sci. Paris 85 (1877), pp. 329–333.
, Comptes Rendus Acad. Sci. Paris 85 (1877), pp. 329–333.
External links
|
|||||||||||||||||||||||||||||